The Secret to Kepler's Harmony of the Planets

This article is somewhat of a departure from the usual article on this blog, anyone interested in physics, astronomy or mathematics might find it interesting. 

by Owen Martin

The solar system is based around circular motion , but as I will now demonstrate, the mechanism by which it's bodies move in relation to the Sun is based on the triangle. Astronomer and mathematician, Johannes Kepler, stumbled upon the idea that a trianglular mechanism governed how the planets moved in 1595 while in the middle of a lecture on the conjunctions of Saturn and Jupiter. Each set of three points he wrote on the blackboard corresponded to a conjunction and formed almost  precise equilateral triangles. These triangles rotated around the board to form two circles, with the radius of one half that of the other one, approximating to the distances of Jupiter and Saturn. 

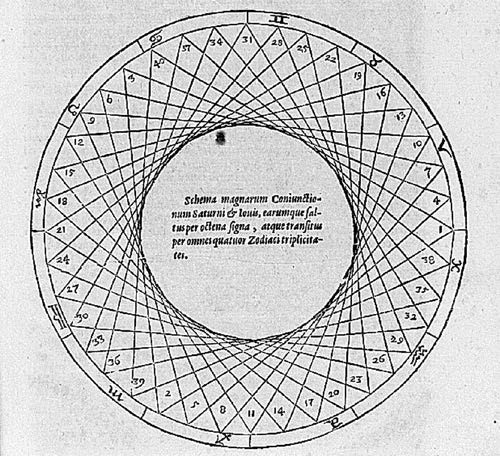
Thus, a triangular pattern determined the distances between two planets moving with a circular motion. This may have something to do with the fact that a circle is constructed using three points just like a triangle. He was then inspired by this discovery to attempt to fit the five Platonic polyhedra solids into an arrangement that corresponded to the known distances at the time between the six known planets. His completed model, published in Mysterium Cosmographicum, was magnificent but a little bit on the complex side (and proven to be a failure over time when greater measurements were found). He actually missed out on something much simpler and even more remarkable. He could have realised this after 1619, when he discovered his third law, published in Harmonices Mundi, the Harmony of the Planets,  but at that stage his focus had shifted to the musical harmony of the planets. 

Keplers Third Law, arguably his greatest discovery, states that the ratio of the squares of the orbital periods of two planets is proportional to the ratio of the cubes of their average distances from the Sun. This applies to all bodies in the solar system, including the moons on Jupiter. It became an accepted law of physics and Isaac Newton later used it to derive his laws of gravitation. It means that the planets do not move in an arbitrary way, but rather according to a finely tuned mathematical formula. 

D³ 𝞪 T²

So if the distance of a planet from the Sun is doubled,

2³ = T²

T² = 8

T = √ 8

The change in the orbital period is the square root of eight or 2.82. The planet will take 2.82 times longer to travel around the Sun.

Now we can work out the change in velocity. Remember the formula, speed equals distance over time from school ?


V = D / T

V = 2 / √ 8

V = 2 / 2.82

V = 0.707

This means the velocity of planet B will be around 70% that of planet A, if B's distance is double that of A's from the sun. In the solar system, Mars is approximately double the distance of Venus, and Uranus is double the distance of Saturn from the Sun and we see that their respective orbital periods and velocities differ by the above ratios.


So, to sum up when:

Distance = x 2

Orbital Period = √ 8

Velocity = 0.707 


The great beauty of these numbers is that they are represented perfectly by Pythagoras's famous right angle Triangle. Once again, remember from school, the square on the hypotenuse is equal to the sum of the squares on the other two sides. If the two sides are both two, then the longer side (hypotenuse) is equal to the square root of  2² + 2², i.e. √ 8, thus representing the change in orbital period.

The connecting line between the 90 degree angle and the centre of the hypotenuse is equal to half of √ 8 or 1.41.

1.41 divided by the side representing distance 2, equals 0.707. Thus this centre line represents the change in velocity.

Also, interesting to note that Sine 45 degrees also gives 0.707 ( sine equals the opposite line over the longer line, the hypotenuse).

So, the solar system is not based on a complex polyhedral system as Kepler believed, but is actually based around the much simpler Triangle. The secret to the Harmony of the Planets and the Mysterium Cosmographicum lies not with Plato and his solids but with the first known Greek mathematician and philosopher, Pythagoras of Samos, and his right angled triangle.

This means that the mechanics of celestial motion has been fine-tuned in accordance with the dimensions of a right angled triangle. The builders of the pyramids (which Pythagoras may have visited) would surely have been satisfied.